Bernoulli, Johann I(Mathematiker, Mechaniker, Arzt)geb.: 06.08.1667 Basel,gest.: 13.01.1748 Basel; |

|
Wichtig für die Analysis ist Bernoullis Funktionsbegriff, auf dem später Euler aufbaute: "Man nennt Funktion einer veränderlichen Größe eine Größe, die auf irgendeine Weise aus eben dieser veränderlichen Größe und Konstanten zusammengesetzt ist." (1718). Dabei ist mit "auf irgendeine Weise" die Anwendung der üblichen arithmetischen Operationen gemeint. Bernoulli schrieb fx, Euler später f(x). Obwohl Bernoulli etwa 1702 den Zusammenhang der Funktionen arctan x und log x über imaginäre Argumente erkannte, entging ihm die unendliche Vieldeutigkeit des Logarithmus. Die berühmte Kontroverse (1712/13) zwischen Bernoulli und Leibniz über den Logarithmus bei negativen Argumenten klärte erst Euler 1749, indem er die Vieldeutigkeit von log x klar erkannte. Eine Domäne Bernoullis war die Infinitesimalrechnung. Zwar hatte Jakob I Bernoulli 1690 zuerst das Wort Integral benutzt, Leibniz ersetzte jedoch auf Vorschlag Bernoullis die Bezeichnung calculus summatoris durch calculus integralis. 1691/92 verfasste Bernoulli eine Integralrechnung. Die Behandlung des Problems der schwingenden Saite (Taylor, 1715) durch Bernoulli 1728 zeigte deutlich die volle Bedeutung des Integrals als Grundbegriff der Analysis, das bis dahin mehr als Hilfsbegriff fungiert hatte.
Eng verbunden sind Bernoullis Leistungen mit der Herausbildung der Variationsrechnung. 1694 stellte er, von Leibniz angeregt, das Problem der isogonalen und orthogonalen Trajektorien einer Kurvenschar und schloss 1697 weitere geometrische Aufgaben an, bei denen er den Zusammenhang mit der Wellentheorie von C. Huygens herausstellte. Diese Aufgaben regten Jakob I Bernoulli zu Arbeiten über geodätische Kurvenscharen an. 1696 stellte Bernoulli das berühmte Brachistochronenproblem: Auf welcher Bahn bewegt sich in einer vertikalen Ebene ein Massepunkt von A nach B vermöge der Schwerkraft in kürzester Zeit? Seine eigene Lösung, die vom intuitiv erfassten Zusammenhang mit der Optik ausging, publizierte er erst 1708, jedoch löste er die am Ende von Jakobs I Bernoullis Lösung gestellten neuen Aufgaben sofort, aber falsch. Erst nachdem Bernoulli 1716 Taylor des Plagiats der Bernoullischen Reihe bezichtigte, wurde er zur erneuten Behandlung der Variationsaufgaben angeregt, vereinfachte und berichtigte den Beweis und fand die zum Problem gehörige Eulersche Differentialgleichung mit der richtigen Ordnung. Bernoullis geometrische Ideen entwickelte erst 1904 C. Caratheodory fruchtbar weiter. Der geometrische Begriff des Richtungsfeldes einer Differentialgleichung geht auf Bernoulli zurück (1694). Nach der komplizierten Lösung der Bernoullischen Differentialgleichung durch Jakob I Bernoulli gab Bernoulli einen eleganten Produktansatz. Um 1710 berechnete er näherungsweise den Umfang einer Ellipse. Ab 1715 benutzte Bernoulli, wie J. Hudde bereits 1657, Raumkoordinaten, wenn auch die systematische Durcharbeitung erst Euler 1748 leistete. 1737 erriet Bernoulli anhand des Ergebnisses einen Beweis Eulers für die Summe der reziproken Quadratzahlen und lieferte einen weiteren Beweis als Nachentdeckung. 1742 gab Bernoulli einen rein geometrischen Beweis für die Produktgleichheit von je 3 überspringenden Abschnitten auf Dreiecksseiten, die durch 3 sich schneidende Ecktransversalen erzeugt werden (Satz von G. Ceva).
In Basel begann Bernoulli ab 1710 die neue Analysis erfolgreich auf die Physik, insbesondere Mechanik und Hydraulik, anzuwenden, was schließlich im Vordergrund seiner Arbeiten stand. Die Kepler-Bewegung und die Neigung der Planetenbahnen gegen den Sonnenäquator leitete Bernoulli aus der Descartesschen Wirbeltheorie ab (Pariser Akademiepreise von 1730 und 1734). Als Anhänger der mechanischen Auffassungen von R. Descartes behinderte Bernoulli die Verbreitung der Newtonschen Theorie (Maupertuis, Voltaire), er versuchte aber besonders in astrophysikalischen Fragen, einen Ausgleich zu erzielen ("Nouvelle physique celeste", 1743). Aus Bernoullis Pariser Zeit stammt dessen Interesse an Newtons Werk. Er arbeitete die "Principia" durch und korrigierte eine Reihe von Fehlern Newtons (u.a. falsche Definition höherer Differentiale).
Zu Bernoullis Zeit waren die Prinzipien der Mechanik zur Ableitung von Differentialgleichungen noch unzureichend ausgearbeitet. Bernoulli erkannte die Bedeutung des Energiebegriffs im physikalischen Sinn (Energiesatz für konservative mechanische Systeme), er formulierte das Prinzip der virtuellen Geschwindigkeiten, eine Konsequenz aus dem Energiesatz, und wandte es beispielsweise auf die Dynamik fester Körper an. 1743 fand er die Bewegungsgleichung eines mechanischen Systems, das kleine Schwingungen ausführt. Aus dem Kraftgesetz, Flächensatz und Energiesatz ermittelte er die entsprechenden Bahnkurven; aus den Bahnkurven und dem Widerstandsgesetz fand er wiederum die zugehörige Zentralkraft (nach 1710). Der Durchbruch in der Behandlung hydromechanischer Probleme gelang Bernoulli und seinem Sohn Daniel Bernoulli unabhängig voneinander, wobei der Vater die "Hydraulik" erstmals aus mechanischen Prinzipien ableitete. Bernoullis Strudelhypothese regte Euler zur Aufstellung der sogenannten Newtonschen Differentialgleichung
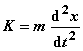
an. In einem Essai von 1714 korrigierte Bernoulli die Schiffstheorie von R. dŽEli-Cagaray (1652 - 1719) aus dem Jahre 1679. Die 1695 von J. Sauver (1653 - 1716) gestellte technische Aufgabe, die Führung des Gewichts einer Klappbrücke zu finden, löste Bernoulli bereits im gleichen Jahr allgemeiner.