Symmetrieeigenschaften der Sinus- und Kosinuszeitfunktionen
Die Kosinuszeitfunktion ist eine achsensymmetrische (gerade) Funktionf(t) = f(-t):
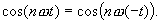
Die Sinuszeitfunktion ist eine nullpunktsymmetrische (ungerade) Funktion
f(t) = -f(-t):
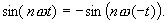
Für ungeradzahlige n haben die Kosinus- und Sinuszeitfunktionen die Eigenschaft der Halbwellensymmetrie 1. Art f(t + T/2) = -f(t):
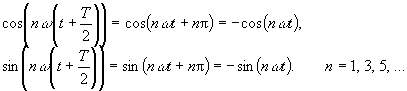
Für geradzahlige n haben die Kosinus- und Sinuszeitfunktionen die Eigenschaft der Halbwellensymmetrie 2. Art f(t + T/2) = f(t):
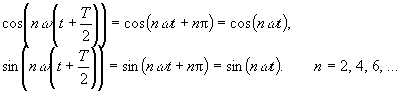
Zur Visualisierung obiger Aussagen können die Sinus- und Kosinuszeitfunktionen für verschiedene n dargestellt werden.