Aufgaben

Aufgabe 1.1
Von einer Schwingung sind folgende Fourierkoeffizienten gegeben:
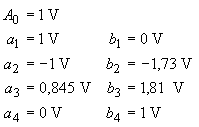a) Ermitteln Sie die Amplituden und Nullphasenwinkel der Harmonischen. Zeichnen Sie die Amplituden- und Phasenspektren der reellen und komplexen Fourierreihe. Stellen Sie die Schwingung dar (Mischpult).

b) Jemand hat bei sonst richtigen Werten für die 2. Harmonische den Phasenwinkel φ 2 = 30° (falsch!) berechnet.
Zeigen Sie diese Schwingung im Mischpult an und vergleichen Sie.

Hilfe bei der Lösung der AufgabeMöglichkeiten zur Uberprüfung Ihrer Lösungmischpult