Dirichlet, Johann Peter Gustav(actually Lejeune Dirichlet, J. P. G.)born: 13.02.1805 Düren (near Aachen)died: 05.05.1859 Göttingen |

|
Dirichlet was the son of a postal commissioner in Düren. His ancestors were from Richelet, a town near Verviers (Belgium) which is why his name "Lejeune Dirichlet" might mean "the young man form Richelet". He recieved his mathematical training in Paris where lived from 1822 to 1826. During that those years he was in constant contact with important mathematicians such as Fourier, Poisson and Lacroix.
Among his pupils were such significant mathematicians as Kummer, Eisenstein, Kronecker, Riemann and Dedekind.
Taking up Fourier's thoughts, Dirichlet provided a proof of convergence for the possibility of the production of periodic , partly continuous and monotonic functions of a real variable according to trigonometric functions.
He solved marginal problems of the potential equation of P.S. Laplace and published articles on hydrodynamics.
He solved the marginal problem by using the Dirichlet principle. This principle defines the minimization of an integral which has the form
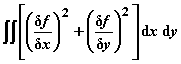
for plane problems.
Among his pupils were such significant mathematicians as Kummer, Eisenstein, Kronecker, Riemann and Dedekind.
Taking up Fourier's thoughts, Dirichlet provided a proof of convergence for the possibility of the production of periodic , partly continuous and monotonic functions of a real variable according to trigonometric functions.
He solved marginal problems of the potential equation of P.S. Laplace and published articles on hydrodynamics.
He solved the marginal problem by using the Dirichlet principle. This principle defines the minimization of an integral which has the form
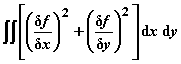
for plane problems.