Symmetry properties of sine and cosine functions
The cosine is a even numbered function which has axial symmetryf(t) = f(-t):
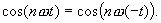
The sine function is a odd numbered function which is symmetrical to the origin
f(t) = -f(-t):
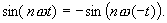
For odd numbered n the sine and cosine functions have the property of half wave symmetry of the first degree f(t + T/2) = -f(t):
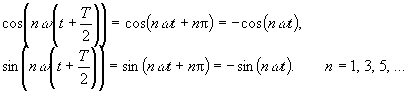
For even numbered n the sine and the cosine function have the property of half wave symmetry of the second degree f(t + T/2) = f(t):
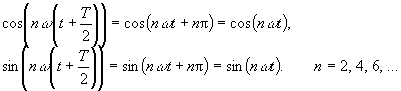
As a visualisation for the statements above sine and cosine functions for various n can be generated here: